I spent the last two weeks of August at a NEH workshop on Networks and Network Analysis for the Humanities, held at the Institute for Pure and Applied Mathematics at UCLA. In a nutshell, the workshop was designed to get humanities scholars in conversation with some of the tool designers, scientists and others who have extensive experience with mapping quantities visually.

James Abello (Rutgers) talks us through the finer points of network topology
Representatives from industry included Yahoo!, Google and Facebook, each talking about how network analysis applied to their data sets.
Video sharing sites such as YouTube provide an interesting testbed for mapping how links spread through communities. How do we know when a video is about to 'go viral', and what is the pattern of hits that differentiates a worldwide hit from a clip with lower interest? We might think about terms and concepts such as Clustering Coëfficient: are users are connected to each other? Overlap: are clusters of users connected to each other? By how many links? In human social networks, this measure of Overlap is often used in determining trust between groups: the more links, the greater the trust. Users who link two different clusters together are called Bridges. One way of quantifying a Bridge is calling it a 'Bridge of degree n'. If a Bridge is deleted or otherwise lost, the number of 'hops' (degrees of separation) is increased by n.
Other work showcased during the workshop focussed on the problem of inferring unknown aspects of a given node. Though this technique is most often used with scientific, rather than social data, a way of describing the concept in human terms is politics. Users might have a higher probability of being a Democrat if all their social connections are with other Democrats, and vice-versa. The term homophily (and anti-homophily) describes nodes' tendency to associate with similar nodes, to greater or lesser degrees.
Of course, all the graph theory in the world won't help if you don't have a good basis for understanding the links between nodes. How do we fit the notoriously subjective humanities into the quantitative world of network analysis? As the above example shows, a lot of the history of the field has been on prediction, which is important for medical and engineering fields. But people working in the humanities want to explore and understand material, rather than predict it. This was the point of David Blei, a computer scientist from Princeton who gave a talk on statistical machine learning methods. Blei described Relational Topic Models, which are built upon Bayesian mixed membership models of discrete data.
Relational Topic Models use topic proportions instead of raw word count -- in essence, they work with a lower-dimensional representation of the object you are studying. This technique can be especially useful in network analysis of complex cultural artifacts such as novels and longer prose. Put simply, Blei's work asks us to consider "both links and attributes" of network nodes. Novels are perhaps the best example of data with more attributes than links: they rarely 'cite' one another, unlike academic papers, but are chock full of linguistic terms which can be analyzed.
Here's a concrete example of some humanities data where Blei's Relational Topic Model could generate an interesting network graph: articles in the journal Scandinavian Studies. Published for over 100 years, the journal has a wealth of information an all sorts of topics, from 19th-century literature to medieval sagas. Let's take an example of the latter, drawn from a database I'm developing of every article and book review in the journal:
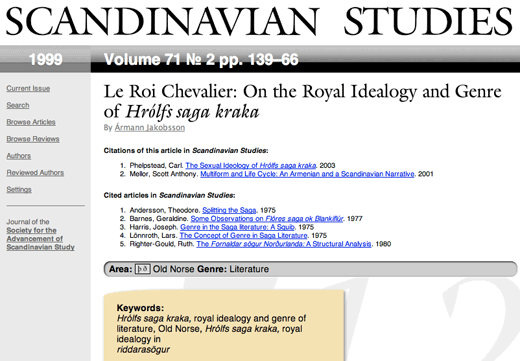
We have two kinds of information about this article: links and attributes.
Links are, for the purposes of this example, both the citations of older writing as well as the citations of this article itself after publication.
Attributes might be explicit subject keywords (Old Norse, Medieval Studies, Iceland, etc), but could also be a vector matrix of term frequency drawn from the text of the article itself. How often does the author use words such as king, genre, etc? Once we know the term frequency for every important word in the text (ignoring "the" and other common words), we can normalize that frequency across a common set of texts (other articles in this and other journals) and come up with a quantitative measure relative similarity.
With both link and attribute data, we might be able to place individual articles into conversation with others, showing networks of influence and the progression of thought across the decades. In the image below (which -- caveat! -- was generated purely from citation links, not any kind of textual attributes), we can see the ways in which older articles "feed into" newer articles through citations.
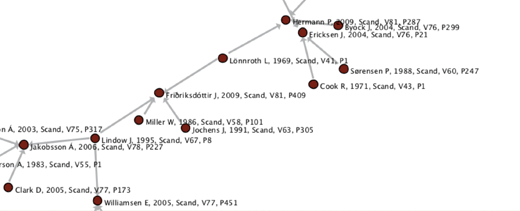
Analyzing such link and attribute data on a large scale, within the context of network theories from academics such as Blei, Abello and others, can lead to a whole new way of understanding and visualizing the humanities. The example above is drawn from scholarly writing, but could well be applied primary sources as well. (Instead of paper citations as link data, we might use extrinsic historic information, such as membership in a salon, circle of thinkers, or commonly-accepted schools of thought.)
One thing the NEH workshop left us all with, I think, is a sense of the rapid pace of innovation in the quantitative world of computer science which drives the field of Network Analysis. It's a daunting thought to consider how much linear algebra and other subjects that humanists will need to be conversant with, in order to truly understand the algorithms that they may be working with in the future. Other fields in the natural and social sciences, such as epidemiology and psychology, have evolved professional models where dedicated statisticians take care of the heavy lifting required by large data sets. Will the humanities do the same? And if so, what kinds of funding would be required to ensure that literature departments could afford such expertise? We would be foolish, surely, to embrace the resource-intensive research methods of quantitative fields such as engineering or computer science without a concomitant strategy for ensuring the longevity and sustainability of such new approaches. No matter how compelling the visual evidence they produce may be.